本日は満月だった(旧暦十六夜)。あいにくの薄曇りだったが、薄い雲から透けて見える満月は妖艶な趣きがあった。。。
(思考実験:2021/04/25sun ~ 2021/04/27tue)
今回のテーマは「光子」と「電磁波」に絞って考える。波全般の挙動を「一般化」するのは、もうちょっと先の課題としたい。
以前、「距離の2乗」をテーマにした記事で、波の振幅を「素粒子の個数」が現れたもの…と書いた(個人的な仮説だが)。が、波長の説明はモヤッとした表現でお茶を濁した。
でも、光子単体のエネルギーに違いがあるとは思えないのに、実際には「波長の違い」というエネルギー強度の違いがあるのは、よく考えれば不思議に感じる筈だ。今回はそれについて考える。
が、それを説明するには予備知識がまだ不十分だ。そこで、特に重要な予備知識を仕込んでおきたい。
波は「素粒子が空間に作用する事」で生まれる。そう考えると、波の波源は素粒子のエネルギーだ。電磁波の場合、光子が波源という事になる。しかし、1個の光子に「波の振幅と波長を決める個体差」があるとは、どうしても思えない。
既に、波の振幅は「素粒子の数」で決まると自分は結論付けている。その時に紹介した図(俯瞰図)と、新たに作図した断面図を以下に示す。
【距離の2乗に比例して光が弱まる俯瞰図】 (光源)16 →|0 4 →|0 0 2| | | 4 | 0 2| | |44 |00 2| | | | 2| | | |2222 | (pi * r^2)/4 = 4分の1円弧の面積の中を拡散 しながら光子は進行する。
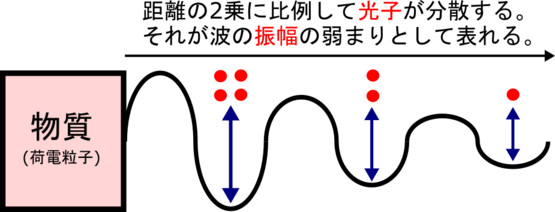
振幅の断面図.png
(編集環境が貧弱なので、曲線がイビツになってしまった…自分の Windowsマシンが復活すれば、こんなもの、自作 script-fu で簡単に作図できるのだが)
つまり、電磁波の本当の波源は「光子の出発地点」の方だったと予想できる。それは、断面図の左端にある「物質(荷電粒子)」の事である。そこで今回の最初のテーマは…
光子はどこから来て、そしてどこへ行くのか。
…という話になる。
黒体輻射(黒体放射):
光子は荷電粒子(物質)から放射され、荷電粒子に吸収される性質がある。特に電子と衝突し易いと考えられていて、それが宇宙の晴れ上がりの原因とされている。
光子がエネルギ-の実体である事は誰も異論はないと思うが、その光子は荷電粒子(電子・陽子を含む物質)から放射される。つまり、荷電粒子自身も内部エネルギ-を持っている。「エネルギ-実体」は光子だけの専売特許ではなく、荷電粒子もエネルギ-実体といえる。
自分の仮説では、荷電粒子は3次元空間のエネルギー実体で、光子は2次元空間のエネルギー実体と考えている。
さて、荷電粒子とは、簡単に言えば「物質」の事。物質には必ず、電荷を持った「電子・陽子」が含まれるので物質は荷電粒子な訳。で、物質は常に光子を放射している。そのため、全ての物質は固有の熱を出している。これを黒体放射(黒体輻射)と呼ぶ。
光子はエネルギー実体なので、物質が黒体放射を続けたら、いずれエネルギーを使い果たして物質は消滅するのでは? と思うだろうが、そうはならない。なぜなら、物質は黒体放射と同時にエネルギーの吸収も行っているから。
むしろ、黒体放射は「外部からの刺激」の副作用だと自分は考えている。その、外部からの刺激こそ「ビッグバン」だと自分は考えている。宇宙には、ビッグバンのエネルギーが光子という形で充満していると考える。だから物質には、常に光子が供給され続ける。
つまり、供給されたエネルギーが、そのまま黒体放射のエネルギーになっていると考える訳。で、物質自身にも内部エネルギーが存在しているので、そのエネルギーが吸収した光子を再び放射するエネルギーに転換し、黒体放射が実現するのだと解釈する。物質がエネルギーを「吸収しっ放し」ではいられないのは、そのためと考える。
で、物質が吸収できるエネルギーには許容量があり、許容量を超えたエネルギーに当てられた物質は急激に発熱し、最終的に発火・融解・蒸発する。これは黒体放射の波長の変化として現れる。つまり、エネルギー収支のバランスが崩れた時に、波長は変化すると解釈できる。
という訳で、光子は荷電粒子から放射される。光子には「荷電粒子という出発地点」がある事が理解できたと思う。これで発射地点(荷電粒子)と光子の相対的な位置関係が語れるようになった。これを波の「振幅」と「波長」を説明する土台とする(個人的な仮説だけど)。
仮説の結論:
電磁波の波長と振幅を決めるのは「黒体放射」のエネルギーだと解釈…
自分が考えた結論はこうだ。波長の違いは「光子の発射間隔」が現れたもの…それしかない(と自分は考える)。発射間隔によって空間の振動数が決まる。それが波長として具現化されると考える。
で、光子が等間隔で放射される理由は、時間という次元にも「量子的な最小単位がある」と仮定したからだ。つまり黒体放射は時計として使える。光子が放射される間隔は、放射元のエネルギーが大きいほど短くなる(早くなる)。
それを「エネルギーを受け取る側」から見ると、エネルギーの授受間隔が短くなるから結果的にエネルギー強度が増す…となる。
電磁波の振幅は光の明るさを表し、それは「同時に放射される光子の数」で決まるが、距離に応じて分散されるので次第に弱まる。一方、波長は放射間隔が短くなるほど「エネルギーが1点集中」されて届くので、力の分散が起きにくい。
銃に例えれば「振幅は散弾銃」「波長はマシンガン」だ。つまり電磁波とは、散弾を連射するマシンガンなのだ。波長の違いを図で表すと次のようになる。
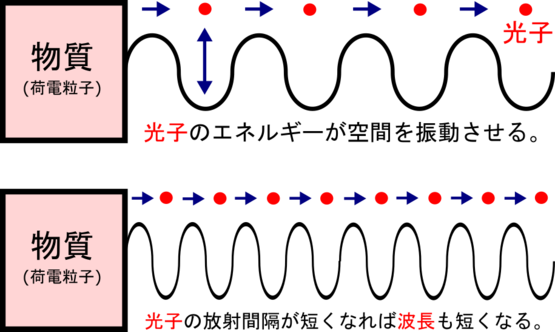
波長.png
さて、光子が一定間隔で発射された場合、どの光子も常に光速で移動するので、個々の光子の間隔が途中で狭くなったり広がったりする事はあり得ない。空間に居る光子は減速も加速もできない。しかも止まれない。
だからこそ、距離に関わらず「波長不変」なのだと考える。これは「複数の光子同士の相対速度は常に 0」である事を示している。が、これは光子の進行する向きが同一平面上の場合に限定されると自分は考えた。
向きが同じ場合は、その光子群は「同一平面上に存在している」と解釈するのだ。自分が平面にこだわる理由は、電磁気力に由来する光子の運動範囲が「量子的に区切られた平面」に限定されると考えているから。
一方、別空間に存在する光子同士の相対速度は「常に光速に固定」されて近づいたり遠ざかったりすると解釈する。これは「物質と光子の相対速度は常に光速に固定される」という現象と一致する。
で、別空間に居る光子同士はお互いに干渉できないと考える。その場合、相対速度が光速で近づく光子が衝突する事はない。
要するに、2次元空間の中だけで帰結する物理現象と、2次元と3次元が相互干渉する物理現象には違いが生じると自分は考えた。で、光子同士の相対速度には「0」の時と「光速」の時の2通りが存在すると考えた訳。
つまり、光子群の相対速度が 0 の時だけ「波長」が観測可能になり、それによって電磁波が具現化されると自分は考えた。逆に、電磁波として知覚できない光子が宇宙にはランダムに飛び交っていて、それが先述の「黒体放射」のエネルギー源になっていると自分は予想した。
一般常識として波は合成できる。が、それは3次元空間に居る人間には、複数の2次元空間を区別できないために「そのようにしか観測できない」と考える。
波の合成によって一瞬「三角波」ができたとしても、それがその後の素粒子の挙動に変化を及ぼす事はない。波の合成は「一過性」のものに過ぎない。衝突したエネルギー波は何事もなく、ただ素通りするだけ。
ただし、波の振動は「電磁気力」や「重力」の起源と考えられるので、光子自体のエネルギーは変化せずとも、空間の「場」に対しては力が作用すると予想できる。
すると、宇宙を行きかっている無数の光子は、他の光子に追いつく事も衝突する事もできない…割と孤独な存在だと解釈できる。自分の考えでは、光子は空間に対して常に斥力を持つので、2つの光子の間に空間が挟まっている限り、光子同士が衝突する事は不可能と考える。
そもそも、光速で移動する素粒子は質量 0 と考えられている。つまり、素粒子はエネルギーを具象化した「仮の粒子」なので、3次元空間で観測される「衝突」という物理現象とは無縁の存在と捉える事もできる。
このトピックでは、光子同士の相対速度が「0」と「光速」の2通りあると仮定し、その理由を、複数の2次元空間の相互作用に求めただけの話。もっと説得力がある理論が存在するなら、素直にそれに従いたいと思っている。
複数個の光子の運動を「振幅や波長の起源」と関連付けて考えようとするのは、むしろ自然な発想だと思う。これらの現象を踏まえた上で、一般化した波の波長と振幅を説明する必要がある。そこに「素粒子と空間の相互作用」があるのは誰もが気付くだろう。
先ほど、光子同士が衝突・干渉する事はないと考えたが、その一方で、光子は3次元の物質に吸収されて光速の旅を終える。これを光子の視点で見ると、物質とは別次元・別空間へ接続するターミナルのようなものになる。
今回はここまでとするが、それでも、かなり示唆に富んだ内容になったと思っている。